pacman::p_load(sf, tidyverse, tmap, corrplot,
ggpubr,spdep,rgdal, funModeling,
blorr,plotly,GWmodel, skimr, caret)Modeling the spatial variation of explanatory factors of waterpoint status using Geographically Weighted Logistic Regression
1. Introduction
The objective of this exercise is to model the spatial variation of explanatory factors of waterpoint status using Geographically Weighted Logistic Regression in Osun state, Nigeria.
What is Geographically Weighted Regression?
It is a spatial statistical technique that takes non-stationary variables into consideration (e.g., climate; demographic factors; physical environment characteristics) and models the local relationships between these independent variables and an outcome of interest (also known as dependent variable).
2. Data
Following two data sets are used:
Osun subzone boundary shapefile in rds format
Osun waterpoint details in rds format
3.Deep Dive into Map Analysis
3.1 Installing libraries and Importing files
Loading packages
Let us first load required packages into R environment. p_load function pf pacman package is used to install the packages
The code chunk below is used to import osun.rds and osun_wp_sf.rds using read_rds() function
osun <- read_rds("data5/rds/Osun.rds")
osun_wp_sf <- read_rds("data5/rds/Osun_wp_sf.rds")3.2 Data Wrangling
Dependent variable - Water point status
Independent variable -
distance_to_primary_road
distance_to_secondary_road
distance_to_tertiary_road
distance_to_city
distance_to_town
water_point_population
local_population_1km
usage_capacity
is_urban
water_source_clean
3.3 Exploratory Data Analysis (EDA)
What is the distribution of independent variable?
osun_wp_sf %>%
freq(input = "status")Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
"none")` instead.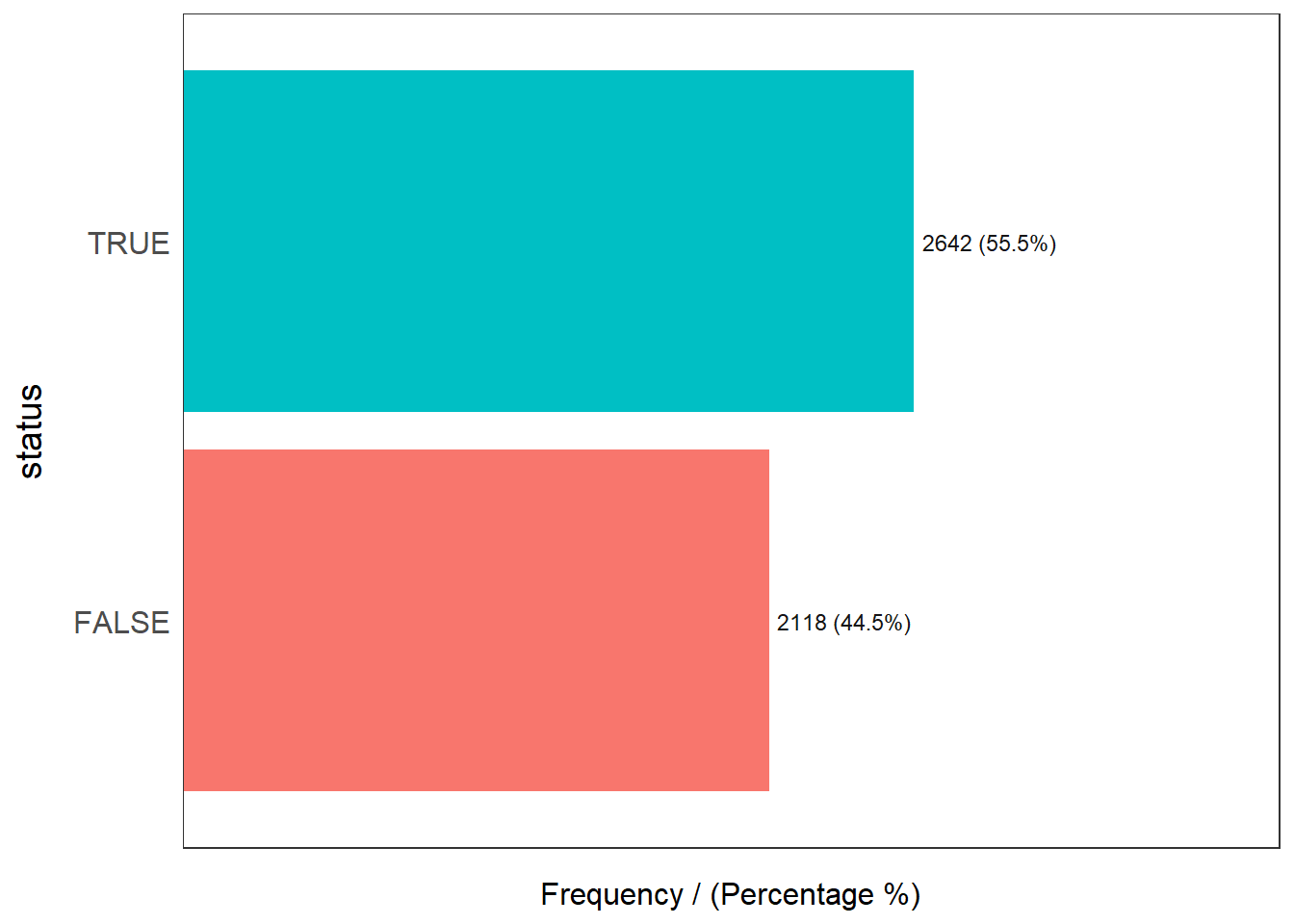
status frequency percentage cumulative_perc
1 TRUE 2642 55.5 55.5
2 FALSE 2118 44.5 100.0What is the overall statistical summary of Osun waterpoints?
osun_wp_sf %>%
skim()Warning: Couldn't find skimmers for class: sfc_POINT, sfc; No user-defined `sfl`
provided. Falling back to `character`.| Name | Piped data |
| Number of rows | 4760 |
| Number of columns | 75 |
| _______________________ | |
| Column type frequency: | |
| character | 47 |
| logical | 5 |
| numeric | 23 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| source | 0 | 1.00 | 5 | 44 | 0 | 2 | 0 |
| report_date | 0 | 1.00 | 22 | 22 | 0 | 42 | 0 |
| status_id | 0 | 1.00 | 2 | 7 | 0 | 3 | 0 |
| water_source_clean | 0 | 1.00 | 8 | 22 | 0 | 3 | 0 |
| water_source_category | 0 | 1.00 | 4 | 6 | 0 | 2 | 0 |
| water_tech_clean | 24 | 0.99 | 9 | 23 | 0 | 3 | 0 |
| water_tech_category | 24 | 0.99 | 9 | 15 | 0 | 2 | 0 |
| facility_type | 0 | 1.00 | 8 | 8 | 0 | 1 | 0 |
| clean_country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| clean_adm1 | 0 | 1.00 | 3 | 5 | 0 | 5 | 0 |
| clean_adm2 | 0 | 1.00 | 3 | 14 | 0 | 35 | 0 |
| clean_adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| clean_adm4 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| installer | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management_clean | 1573 | 0.67 | 5 | 37 | 0 | 7 | 0 |
| status_clean | 0 | 1.00 | 9 | 32 | 0 | 7 | 0 |
| pay | 0 | 1.00 | 2 | 39 | 0 | 7 | 0 |
| fecal_coliform_presence | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| subjective_quality | 0 | 1.00 | 18 | 20 | 0 | 4 | 0 |
| activity_id | 4757 | 0.00 | 36 | 36 | 0 | 3 | 0 |
| scheme_id | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| wpdx_id | 0 | 1.00 | 12 | 12 | 0 | 4760 | 0 |
| notes | 0 | 1.00 | 2 | 96 | 0 | 3502 | 0 |
| orig_lnk | 4757 | 0.00 | 84 | 84 | 0 | 1 | 0 |
| photo_lnk | 41 | 0.99 | 84 | 84 | 0 | 4719 | 0 |
| country_id | 0 | 1.00 | 2 | 2 | 0 | 1 | 0 |
| data_lnk | 0 | 1.00 | 79 | 96 | 0 | 2 | 0 |
| water_point_history | 0 | 1.00 | 142 | 834 | 0 | 4750 | 0 |
| clean_country_id | 0 | 1.00 | 3 | 3 | 0 | 1 | 0 |
| country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| water_source | 0 | 1.00 | 8 | 30 | 0 | 4 | 0 |
| water_tech | 0 | 1.00 | 5 | 37 | 0 | 20 | 0 |
| adm2 | 0 | 1.00 | 3 | 14 | 0 | 33 | 0 |
| adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management | 1573 | 0.67 | 5 | 47 | 0 | 7 | 0 |
| adm1 | 0 | 1.00 | 4 | 5 | 0 | 4 | 0 |
| New Georeferenced Column | 0 | 1.00 | 16 | 35 | 0 | 4760 | 0 |
| lat_lon_deg | 0 | 1.00 | 13 | 32 | 0 | 4760 | 0 |
| public_data_source | 0 | 1.00 | 84 | 102 | 0 | 2 | 0 |
| converted | 0 | 1.00 | 53 | 53 | 0 | 1 | 0 |
| created_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| updated_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| Geometry | 0 | 1.00 | 33 | 37 | 0 | 4760 | 0 |
| ADM2_EN | 0 | 1.00 | 3 | 14 | 0 | 30 | 0 |
| ADM2_PCODE | 0 | 1.00 | 8 | 8 | 0 | 30 | 0 |
| ADM1_EN | 0 | 1.00 | 4 | 4 | 0 | 1 | 0 |
| ADM1_PCODE | 0 | 1.00 | 5 | 5 | 0 | 1 | 0 |
Variable type: logical
| skim_variable | n_missing | complete_rate | mean | count |
|---|---|---|---|---|
| rehab_year | 4760 | 0 | NaN | : |
| rehabilitator | 4760 | 0 | NaN | : |
| is_urban | 0 | 1 | 0.39 | FAL: 2884, TRU: 1876 |
| latest_record | 0 | 1 | 1.00 | TRU: 4760 |
| status | 0 | 1 | 0.56 | TRU: 2642, FAL: 2118 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| row_id | 0 | 1.00 | 68550.48 | 10216.94 | 49601.00 | 66874.75 | 68244.50 | 69562.25 | 471319.00 | ▇▁▁▁▁ |
| lat_deg | 0 | 1.00 | 7.68 | 0.22 | 7.06 | 7.51 | 7.71 | 7.88 | 8.06 | ▁▂▇▇▇ |
| lon_deg | 0 | 1.00 | 4.54 | 0.21 | 4.08 | 4.36 | 4.56 | 4.71 | 5.06 | ▃▆▇▇▂ |
| install_year | 1144 | 0.76 | 2008.63 | 6.04 | 1917.00 | 2006.00 | 2010.00 | 2013.00 | 2015.00 | ▁▁▁▁▇ |
| fecal_coliform_value | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| distance_to_primary_road | 0 | 1.00 | 5021.53 | 5648.34 | 0.01 | 719.36 | 2972.78 | 7314.73 | 26909.86 | ▇▂▁▁▁ |
| distance_to_secondary_road | 0 | 1.00 | 3750.47 | 3938.63 | 0.15 | 460.90 | 2554.25 | 5791.94 | 19559.48 | ▇▃▁▁▁ |
| distance_to_tertiary_road | 0 | 1.00 | 1259.28 | 1680.04 | 0.02 | 121.25 | 521.77 | 1834.42 | 10966.27 | ▇▂▁▁▁ |
| distance_to_city | 0 | 1.00 | 16663.99 | 10960.82 | 53.05 | 7930.75 | 15030.41 | 24255.75 | 47934.34 | ▇▇▆▃▁ |
| distance_to_town | 0 | 1.00 | 16726.59 | 12452.65 | 30.00 | 6876.92 | 12204.53 | 27739.46 | 44020.64 | ▇▅▃▃▂ |
| rehab_priority | 2654 | 0.44 | 489.33 | 1658.81 | 0.00 | 7.00 | 91.50 | 376.25 | 29697.00 | ▇▁▁▁▁ |
| water_point_population | 4 | 1.00 | 513.58 | 1458.92 | 0.00 | 14.00 | 119.00 | 433.25 | 29697.00 | ▇▁▁▁▁ |
| local_population_1km | 4 | 1.00 | 2727.16 | 4189.46 | 0.00 | 176.00 | 1032.00 | 3717.00 | 36118.00 | ▇▁▁▁▁ |
| crucialness_score | 798 | 0.83 | 0.26 | 0.28 | 0.00 | 0.07 | 0.15 | 0.35 | 1.00 | ▇▃▁▁▁ |
| pressure_score | 798 | 0.83 | 1.46 | 4.16 | 0.00 | 0.12 | 0.41 | 1.24 | 93.69 | ▇▁▁▁▁ |
| usage_capacity | 0 | 1.00 | 560.74 | 338.46 | 300.00 | 300.00 | 300.00 | 1000.00 | 1000.00 | ▇▁▁▁▅ |
| days_since_report | 0 | 1.00 | 2692.69 | 41.92 | 1483.00 | 2688.00 | 2693.00 | 2700.00 | 4645.00 | ▁▇▁▁▁ |
| staleness_score | 0 | 1.00 | 42.80 | 0.58 | 23.13 | 42.70 | 42.79 | 42.86 | 62.66 | ▁▁▇▁▁ |
| location_id | 0 | 1.00 | 235865.49 | 6657.60 | 23741.00 | 230638.75 | 236199.50 | 240061.25 | 267454.00 | ▁▁▁▁▇ |
| cluster_size | 0 | 1.00 | 1.05 | 0.25 | 1.00 | 1.00 | 1.00 | 1.00 | 4.00 | ▇▁▁▁▁ |
| lat_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| lon_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| count | 0 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ▁▁▇▁▁ |
Let us now select the desired variables by using filter() function and save it in new dataframe called osun_wp_sf_clean
osun_wp_sf_clean <- osun_wp_sf %>%
filter_at(vars(status,
distance_to_primary_road,
distance_to_secondary_road,
distance_to_tertiary_road,
distance_to_city,
distance_to_town,
water_point_population,
local_population_1km,
usage_capacity,is_urban,
water_source_clean),
all_vars(!is.na(.))) %>%
mutate(usage_capacity = as.factor(usage_capacity))3.4 Correlation Analysis
Before building the model, let us determine if there are highly correlated variables. First, let us drop the geometry column to proceed to correlation nad select only the desired columns
osun_wp <- osun_wp_sf_clean %>%
select(c(7,35:39, 42:43, 46:47, 57)) %>%
st_set_geometry(NULL)cluster_vars.cor = cor(osun_wp[,2:7])
corrplot.mixed(cluster_vars.cor,
lower = "ellipse",
upper = "number",
tl.pos = "lt",
diag = "l",
tl.col = "black")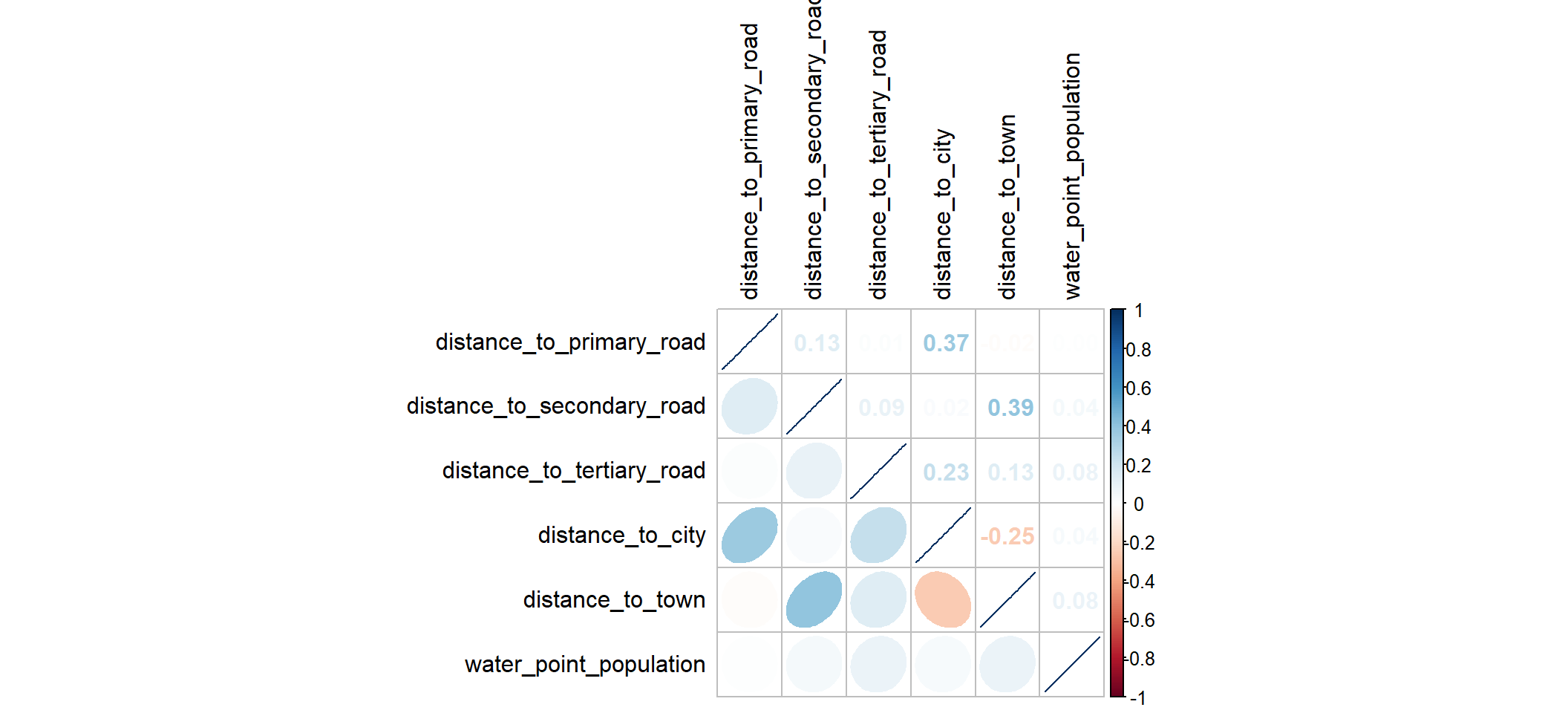
As we can see that correlation coefficent are not greater than 0.8 and hence no variables are highly correlated.Therefore, all variables can be included in building a model.
3.5 Fitting Generalised Linear Models
glm is used to fit generalized linear models, specified by giving a symbolic description of the linear predictor and a description of the error distribution. Instead of using typical R report, Binary logistic regression report is shown using blr_regress() function
model <- glm(status ~ distance_to_primary_road +
distance_to_secondary_road+
distance_to_tertiary_road+
distance_to_city+
distance_to_town+
is_urban+
usage_capacity+
water_source_clean+
water_point_population+
local_population_1km,
data = osun_wp_sf_clean,
family = binomial(link='logit'))
blr_regress(model) Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4744 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3887 0.1124 3.4588 5e-04
distance_to_primary_road 1 0.0000 0.0000 -0.7153 0.4744
distance_to_secondary_road 1 0.0000 0.0000 -0.5530 0.5802
distance_to_tertiary_road 1 1e-04 0.0000 4.6708 0.0000
distance_to_city 1 0.0000 0.0000 -4.7574 0.0000
distance_to_town 1 0.0000 0.0000 -4.9170 0.0000
is_urbanTRUE 1 -0.2971 0.0819 -3.6294 3e-04
usage_capacity1000 1 -0.6230 0.0697 -8.9366 0.0000
water_source_cleanProtected Shallow Well 1 0.5040 0.0857 5.8783 0.0000
water_source_cleanProtected Spring 1 1.2882 0.4388 2.9359 0.0033
water_point_population 1 -5e-04 0.0000 -11.3686 0.0000
local_population_1km 1 3e-04 0.0000 19.2953 0.0000
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7347 Somers' D 0.4693
% Discordant 0.2653 Gamma 0.4693
% Tied 0.0000 Tau-a 0.2318
Pairs 5585188 c 0.7347
---------------------------------------------------------------From the above report we can see that the at 95% confidence, the variables distance_to_primary_road and distance_to_secondary_road are insignificant. Hence, let us exclude those variables whose p values are higher than 0.05 and recalibrate the model.
3.6 Recalibirating the model
remodel <- glm(status ~ distance_to_tertiary_road+
distance_to_city+
distance_to_town+
is_urban+
usage_capacity+
water_source_clean+
water_point_population+
local_population_1km,
data = osun_wp_sf_clean,
family = binomial(link='logit'))
blr_regress(remodel) Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4746 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3540 0.1055 3.3541 8e-04
distance_to_tertiary_road 1 1e-04 0.0000 4.9096 0.0000
distance_to_city 1 0.0000 0.0000 -5.2022 0.0000
distance_to_town 1 0.0000 0.0000 -5.4660 0.0000
is_urbanTRUE 1 -0.2667 0.0747 -3.5690 4e-04
usage_capacity1000 1 -0.6206 0.0697 -8.9081 0.0000
water_source_cleanProtected Shallow Well 1 0.4947 0.0850 5.8228 0.0000
water_source_cleanProtected Spring 1 1.2790 0.4384 2.9174 0.0035
water_point_population 1 -5e-04 0.0000 -11.3902 0.0000
local_population_1km 1 3e-04 0.0000 19.4069 0.0000
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7349 Somers' D 0.4697
% Discordant 0.2651 Gamma 0.4697
% Tied 0.0000 Tau-a 0.2320
Pairs 5585188 c 0.7349
---------------------------------------------------------------Now let us view the confusion matrix with the following evaluation metrics
In binomial logistic regression, the classification table is a 2 x 2 table that contains the observed and predicted model results (shown in the figure below). It is popularly known as contingency table. The table is often called an “error table” or a “confusion matrix”.
The contingency table has 4 data cells:
1. Actual 0 Predicted 0 – The number of cases that were both predicted and observed as 0. The records in this cell are referred to as true negatives. The model classification was correct for these records.
2. Actual 0 Predicted 1 – The number of cases that were predicted as 1 yet observed as 0. The records in this cell are referred to as false positives. The model classification was incorrect for these records.
3. Actual 1 Predicted 1 – The number of cases that were both predicted and observed as 1. The records in this cell are referred to as true positives. The model classification was correct for these records.
4. Actual 1 Predicted 0 – The number of cases that were predicted as 0 yet observed as 1. The records in this cell are referred to as false negatives. The model classification was incorrect for these records.
blr_confusion_matrix(model, cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1301 738
1 813 1904
Accuracy : 0.6739
No Information Rate : 0.4445
Kappa : 0.3373
McNemars's Test P-Value : 0.0602
Sensitivity : 0.7207
Specificity : 0.6154
Pos Pred Value : 0.7008
Neg Pred Value : 0.6381
Prevalence : 0.5555
Detection Rate : 0.4003
Detection Prevalence : 0.5713
Balanced Accuracy : 0.6680
Precision : 0.7008
Recall : 0.7207
'Positive' Class : 1blr_confusion_matrix(remodel, cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1300 743
1 814 1899
Accuracy : 0.6726
No Information Rate : 0.4445
Kappa : 0.3348
McNemars's Test P-Value : 0.0761
Sensitivity : 0.7188
Specificity : 0.6149
Pos Pred Value : 0.7000
Neg Pred Value : 0.6363
Prevalence : 0.5555
Detection Rate : 0.3993
Detection Prevalence : 0.5704
Balanced Accuracy : 0.6669
Precision : 0.7000
Recall : 0.7188
'Positive' Class : 1We can compare the results of both confusion matrices before and after excluding the insignifcant variables. There is not much difference in the results though. It is because in general, when an independent variable is removed from a regression model, the overall explanatory or performance of the model will be compromised. This is the nature of regression models. However, when an insignificant independent variable was removed from the model,the performance of the model will be lesser than when a significant independent was removed from the model. Hence, we have witnessed the same here in this case as the accuracy is 67.26 % later while recalibrating the model when compared to 67.39% previously.
3.7 Converting into spatial dataframe
Let us convert the simple feature dataframe into spatial dataframe using as_spatial() function. The below code chunk performs the conversion
osun_wp_sp <- osun_wp_sf_clean %>%
select(c(status,
distance_to_tertiary_road,
distance_to_city,
distance_to_town,
is_urban,
usage_capacity,
water_source_clean,
water_point_population,
local_population_1km
))%>%
as_Spatial()
osun_wp_spclass : SpatialPointsDataFrame
features : 4756
extent : 182502.4, 290751, 340054.1, 450905.3 (xmin, xmax, ymin, ymax)
crs : +proj=tmerc +lat_0=4 +lon_0=8.5 +k=0.99975 +x_0=670553.98 +y_0=0 +a=6378249.145 +rf=293.465 +towgs84=-92,-93,122,0,0,0,0 +units=m +no_defs
variables : 9
names : status, distance_to_tertiary_road, distance_to_city, distance_to_town, is_urban, usage_capacity, water_source_clean, water_point_population, local_population_1km
min values : 0, 0.017815121653488, 53.0461399623541, 30.0019777713073, 0, 1000, Borehole, 0, 0
max values : 1, 10966.2705628969, 47934.343603562, 44020.6393368124, 1, 300, Protected Spring, 29697, 36118 3.8 Bandwidth selection for Generalised Geographically Weighted Regression (GGWR)
The code chunk below is used to calibrate a generalised GWR model using bw.ggwr() function
bw.fixed <- bw.ggwr(status ~distance_to_tertiary_road+
distance_to_city+
distance_to_town+
is_urban+
usage_capacity+
water_source_clean+
water_point_population+
local_population_1km,
data = osun_wp_sp,
family = "binomial",
approach = "AIC",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)Take a cup of tea and have a break, it will take a few minutes.
-----A kind suggestion from GWmodel development group
Iteration Log-Likelihood:(With bandwidth: 95768.67 )
=========================
0 -2890
1 -2837
2 -2830
3 -2829
4 -2829
5 -2829
Fixed bandwidth: 95768.67 AICc value: 5681.18
Iteration Log-Likelihood:(With bandwidth: 59200.13 )
=========================
0 -2878
1 -2820
2 -2812
3 -2810
4 -2810
5 -2810
Fixed bandwidth: 59200.13 AICc value: 5645.901
Iteration Log-Likelihood:(With bandwidth: 36599.53 )
=========================
0 -2854
1 -2790
2 -2777
3 -2774
4 -2774
5 -2774
6 -2774
Fixed bandwidth: 36599.53 AICc value: 5585.354
Iteration Log-Likelihood:(With bandwidth: 22631.59 )
=========================
0 -2810
1 -2732
2 -2711
3 -2707
4 -2707
5 -2707
6 -2707
Fixed bandwidth: 22631.59 AICc value: 5481.877
Iteration Log-Likelihood:(With bandwidth: 13998.93 )
=========================
0 -2732
1 -2635
2 -2604
3 -2597
4 -2596
5 -2596
6 -2596
Fixed bandwidth: 13998.93 AICc value: 5333.718
Iteration Log-Likelihood:(With bandwidth: 8663.649 )
=========================
0 -2624
1 -2502
2 -2459
3 -2447
4 -2446
5 -2446
6 -2446
7 -2446
Fixed bandwidth: 8663.649 AICc value: 5178.493
Iteration Log-Likelihood:(With bandwidth: 5366.266 )
=========================
0 -2478
1 -2319
2 -2250
3 -2225
4 -2219
5 -2219
6 -2220
7 -2220
8 -2220
9 -2220
Fixed bandwidth: 5366.266 AICc value: 5022.016
Iteration Log-Likelihood:(With bandwidth: 3328.371 )
=========================
0 -2222
1 -2002
2 -1894
3 -1838
4 -1818
5 -1814
6 -1814
Fixed bandwidth: 3328.371 AICc value: 4827.587
Iteration Log-Likelihood:(With bandwidth: 2068.882 )
=========================
0 -1837
1 -1528
2 -1357
3 -1261
4 -1222
5 -1222
Fixed bandwidth: 2068.882 AICc value: 4772.046
Iteration Log-Likelihood:(With bandwidth: 1290.476 )
=========================
0 -1403
1 -1016
2 -807.3
3 -680.2
4 -680.2
Fixed bandwidth: 1290.476 AICc value: 5809.719
Iteration Log-Likelihood:(With bandwidth: 2549.964 )
=========================
0 -2019
1 -1753
2 -1614
3 -1538
4 -1506
5 -1506
Fixed bandwidth: 2549.964 AICc value: 4764.056
Iteration Log-Likelihood:(With bandwidth: 2847.289 )
=========================
0 -2108
1 -1862
2 -1736
3 -1670
4 -1644
5 -1644
Fixed bandwidth: 2847.289 AICc value: 4791.834
Iteration Log-Likelihood:(With bandwidth: 2366.207 )
=========================
0 -1955
1 -1675
2 -1525
3 -1441
4 -1407
5 -1407
Fixed bandwidth: 2366.207 AICc value: 4755.524
Iteration Log-Likelihood:(With bandwidth: 2252.639 )
=========================
0 -1913
1 -1623
2 -1465
3 -1376
4 -1341
5 -1341
Fixed bandwidth: 2252.639 AICc value: 4759.188
Iteration Log-Likelihood:(With bandwidth: 2436.396 )
=========================
0 -1980
1 -1706
2 -1560
3 -1479
4 -1446
5 -1446
Fixed bandwidth: 2436.396 AICc value: 4756.675
Iteration Log-Likelihood:(With bandwidth: 2322.828 )
=========================
0 -1940
1 -1656
2 -1503
3 -1417
4 -1382
5 -1382
Fixed bandwidth: 2322.828 AICc value: 4756.471
Iteration Log-Likelihood:(With bandwidth: 2393.017 )
=========================
0 -1965
1 -1687
2 -1539
3 -1456
4 -1422
5 -1422
Fixed bandwidth: 2393.017 AICc value: 4755.57
Iteration Log-Likelihood:(With bandwidth: 2349.638 )
=========================
0 -1949
1 -1668
2 -1517
3 -1432
4 -1398
5 -1398
Fixed bandwidth: 2349.638 AICc value: 4755.753
Iteration Log-Likelihood:(With bandwidth: 2376.448 )
=========================
0 -1959
1 -1680
2 -1530
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2376.448 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2382.777 )
=========================
0 -1961
1 -1683
2 -1534
3 -1450
4 -1416
5 -1416
Fixed bandwidth: 2382.777 AICc value: 4755.491
Iteration Log-Likelihood:(With bandwidth: 2372.536 )
=========================
0 -1958
1 -1678
2 -1528
3 -1445
4 -1411
5 -1411
Fixed bandwidth: 2372.536 AICc value: 4755.488
Iteration Log-Likelihood:(With bandwidth: 2378.865 )
=========================
0 -1960
1 -1681
2 -1532
3 -1448
4 -1414
5 -1414
Fixed bandwidth: 2378.865 AICc value: 4755.481
Iteration Log-Likelihood:(With bandwidth: 2374.954 )
=========================
0 -1959
1 -1679
2 -1530
3 -1446
4 -1412
5 -1412
Fixed bandwidth: 2374.954 AICc value: 4755.482
Iteration Log-Likelihood:(With bandwidth: 2377.371 )
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2377.371 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2377.942 )
=========================
0 -1960
1 -1680
2 -1531
3 -1448
4 -1414
5 -1414
Fixed bandwidth: 2377.942 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2377.018 )
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2377.018 AICc value: 4755.48 The below code chunk helps us to create generalised models with Binomial option using ggwr.basic() function
gwlr.fixed <- ggwr.basic(status ~distance_to_tertiary_road+
distance_to_city+
distance_to_town+
is_urban+
usage_capacity+
water_source_clean+
water_point_population+
local_population_1km,
data = osun_wp_sp,
bw=bw.fixed,
family="binomial",
kernel="gaussian",
adaptive=FALSE,
longlat = FALSE) Iteration Log-Likelihood
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413 3.9 Converting SDF into sf data.frame
To assess the performance of the gwLR, first let us convert the sdf object in as data frame by using the code chunk below
gwr.fixed <- as.data.frame(gwlr.fixed$SDF)Next, let us label yhat values greater than or equal to 0.5 into 1 and else 0. The result of the logic comparison operation will be saved into a field called most
gwr.fixed <- gwr.fixed %>%
mutate(most = ifelse(gwr.fixed$yhat >=0.5,T,F))gwr.fixed$y <- as.factor(gwr.fixed$y)
gwr.fixed$most <- as.factor(gwr.fixed$most)
CM <- confusionMatrix(data = gwr.fixed$most,
reference= gwr.fixed$y,
positive = "TRUE" )
CMConfusion Matrix and Statistics
Reference
Prediction FALSE TRUE
FALSE 1833 268
TRUE 281 2374
Accuracy : 0.8846
95% CI : (0.8751, 0.8935)
No Information Rate : 0.5555
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7661
Mcnemar's Test P-Value : 0.6085
Sensitivity : 0.8986
Specificity : 0.8671
Pos Pred Value : 0.8942
Neg Pred Value : 0.8724
Prevalence : 0.5555
Detection Rate : 0.4992
Detection Prevalence : 0.5582
Balanced Accuracy : 0.8828
'Positive' Class : TRUE
Thus, for the comparision, we have used argument positive = “TRUE” and accuracy here is 88% and the sensitivity and specificity values are 89% and 86% respectively which means the model is able to identify 89% of right cases correctly and 86% percent of false cases correctly.
osun_wp_sf_selected <- osun_wp_sf_clean %>%
select(c(ADM2_EN, ADM2_PCODE,
ADM1_EN, ADM1_PCODE,
status))Now let us append gwr.fixed matrix onto osun_wp_sf_selected to produce an output simple feature object called gwr_sf.fixed using cbind() function
gwr_sf.fixed <- cbind(osun_wp_sf_selected, gwr.fixed)The estimated or predicted values in a regression or other predictive model are termed the y-hat values. “Y” because y is the outcome or dependent variable in the model equation, and a “hat” symbol (circumflex) placed over the variable name is the statistical designation of an estimated value.
Finally, let us view these yhat values geographically mapped onto Osun division. The lighter the colour lower the yhat value and the darker colour indicates high yhat values i.e predicted values.
tmap_mode("view")tmap mode set to interactive viewingprob_T <- tm_shape(osun)+
tm_polygons(alpha=0.1)+
tm_shape(gwr_sf.fixed)+
tm_dots(col="yhat",
border.col = "gray60",
border.lwd = 1)+
tm_view(set.zoom.limits = c(9,14))
prob_T4. Conclusion
In this study, we have modeled the spatial variation of explanatory factors of waterpoint status using Geographically Weighted Logistic Regression in Osun state, Nigeria by executing various geographically weighted regression models. The confusion matrix and evaluation metrics helped us in undertanding the performance of the model better. Finally, we have mapped the fixed gwr sf values by varying the colours with respect to yhat values.